很多参加过高考数学的人说,解决立体几何问题，关键在于添加辅助线，甚至一些人认为“解立体几何，得辅助线者得天下”。这样的话或许有些夸张，但也表明解决立体几何问题关键在于要学会添加辅助线。

      事实上，如何添加辅助线一直是很多学生学习几何难点和痛点，一些同学由于没有掌握好添加辅助线的基本方法,给解题带来很大的困扰。在添加辅助线过程中，很多同学都是片面凭解题感觉、盲目乱添，不仅没能帮助解决问题，甚至给解题带来错误的引导。

      其实掌握立体几何添加辅助线的方法，大家可以牢记这么一段口诀：“有了中点配中点，两点相连中位线；等腰三角形出现，顶底中点相连线；有了垂面作垂线，水到渠成理当然。”

      今天我们就结合一些实际例题，来讲讲如何解决立体几何问题。

      典型例题1：

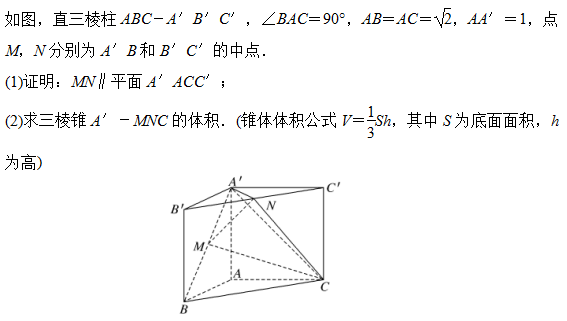
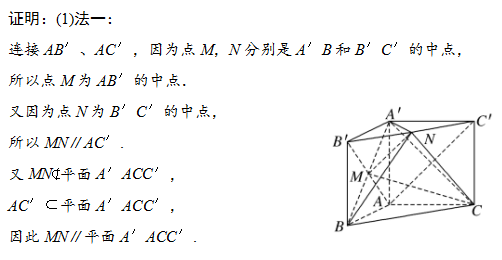
      解决有关线面平行、面面平行的基本问题要注意：

      1、判定定理与性质定理中易忽视的条件，如线面平行的判定定理中条件线在面外易忽视．

      2、结合题意构造或绘制图形，结合图形作出判断．

      3、举反例否定结论或用反证法推断命题是否正确．

      在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而在性质定理的应用中，其顺序恰好相反，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”．

      辅助线(面)是求证平行问题的关键，注意平面几何中位线，平行四边形及相似中有关平行性质的应用．

      典型例题2：

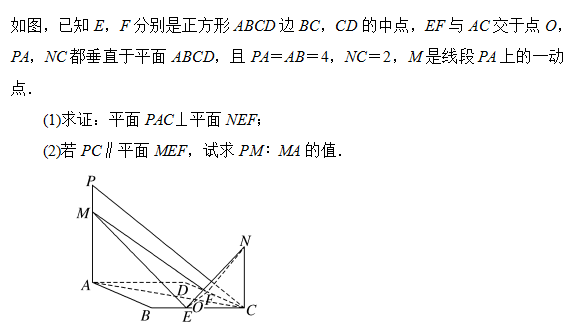
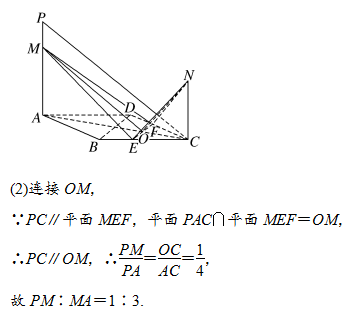
      判定面面垂直的方法：

      1、面面垂直的定义。

      2、面面垂直的判定定理(a⊥β，a?α?α⊥β)．

      在已知平面垂直时，一般要用性质定理进行转化，转化为线面垂直或线线垂直．

      转化方法：在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．

      在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决，如有平面垂直时，一般要用性质定理．

      几个常用的结论：

      1、过空间任一点有且只有一条直线与已知平面垂直．

      2、过空间任一点有且只有一个平面与已知直线垂直．

      解决此类问题常用的方法有：

        ①依据定理条件才能得出结论的，可结合符合题意的图形作出判断；

        ②否定命题时只需举一个反例；

        ③寻找恰当的特殊模型(如构造长方体)进行筛选。

      求异面直线所成的角一般用平移法，步骤如下：

      1、一作：即找或作平行线，作出异面直线所成的角；

      2、二证：即证明作出的角是异面直线所成的角；

      3、三求：解三角形，求出所作的角，如果求出的角是      锐角或直角，则它就是要求的角，如果求出的角是钝角，则它的补角才是要求的角。