导数的运算

1、常见函数的导数公式：

常数函数的导数：；

幂函数的导数：；

如下：

；

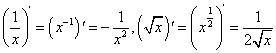
三角函数的导数：；

对数函数的导数：

指数函数的导数：　

2、求导数的法则

（1）和与差函数的导数：．

由此得多项式函数导数

（2）积的函数的导数：,

特例[C·f(x)]'＝Cf'(x)。

如：①已知函数的导数为，则_____（答：）；

②函数的导数为__________（答：）；

③若对任意，，则是______（答：）

（3）商的函数的导数：

例1、求下列导数

（1）y ＝；（2）y ＝x · sin x · ln x；

（3）y ＝；（4）y ＝．

解：（1）∵y ＝＝

∴

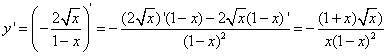
（2）y'＝(x · sin x · ln x) '＝(x · sin x) ' · ln x+(x · sin x )( ln x) '

＝[x'sinx+x(sinx) ']·lnx+(x · sin x )

＝[sinx+xcosx]lnx+sinx

如遇求多个积的导数，可以逐层分组进行；求导数前的变形，目的在于简化运算；求导数后应对结果进行整理化简．

（3）y'＝

（4）∵y ＝＝

∴y'＝

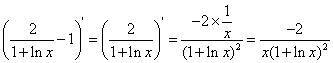
例2、求函数的导数

①y＝（2 x2－5 x ＋1）ex

②y＝

解：①y'＝（2 x2－5 x ＋1）′ex＋（2 x2－5 x ＋1）(ex)′＝(2x2－x－4)ex

②

∴y'

例3、已知曲线C：y ＝3 x 4－2 x3－9 x2＋4

（1）求曲线C上横坐标为1的点的切线方程；

（2）第（1）小题中切线与曲线C是否还有其他公共点？

解：（1）把x ＝1代入C的方程，求得y ＝－4．

∴切点为（1，－4）．

Y'＝12 x3－6 x2－18 x，

∴切线斜率为k ＝12－6－18＝－12．

∴切线方程为y ＋4＝－12（x－1），即

y＝－12 x ＋8．

由

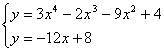
得

3 x 4－2 x3 －9 x2＋12 x －4＝0

(x －1) 2 (x ＋2) (3 x －2)＝0

x ＝1，－2，．

代入y ＝3 x 4－2 x 3 －9 x 2 ＋4，求得y ＝－4，32，0，即公共点为（1，－4）（切点），（－2，32），（，0）．

除切点外，还有两个交点（－2，32）、（，0）．

直线和圆，直线和椭圆相切，可以用只有一个公共点来判定．一般曲线却要用割线的极限位置来定义切线．因此，曲线的切线可以和曲线有非切点的公共点．

例4、曲线S：y ＝x3－6 x 2－x ＋6哪一点切线的斜率最小？

设此点为P（x0，y0）．证明：曲线S关于P中心对称．

解：y'＝3 x2－12 x －1

当x ＝＝2时，y′有最小值，故x 0＝2，

由P∈S知：y 0＝23－6 · 22－2＋6＝－12

即在P（2，－12）处切线斜率最小．

设Q（x，y）∈S，即y ＝x3－6 x2－x ＋6

则与Q关于P对称的点为R（4－x，－24－y），只需证R的坐标满足S的方程即可．

(4－x)3－6(4－x)2－(4－x)＋6

＝64－48 x ＋12 x 2 －x 3－6（16－8 x ＋x2）＋x ＋2

＝－x 3 ＋6 x 2 ＋x －30

＝－x 3 ＋6 x2 ＋x －6－24

＝－y－24

故R∈S，由Q点的任意性，S关于点P中心对称．

求切点时，要将取最小值的x值代回原方程．

例5、一质点的运动方程为s(t)＝asint+bcost(a>0)，若速度v(t)的最大值为，且对任意的t0∈R,在t＝t0与t＝－t0时速度相同，求a、b的值。

解：v(t)＝s(t)＝acost－bsint

∵v(t)的最大值为∴a2+b2＝

又∵在t＝t0与t＝－t0时速度相同

∴(a+b)(cost0－sint0)＝0且对任意的t0∈R且a>0

∴(a+b) ＝0，∴a＝，b＝－

用导数证明不等式，关键在于构造函数，然后在相应区间上用导数的相关知识判别其单调性，再利用单调性得到所证明的不等式。

例1、已知x∈（0，），

求证：sinx＜x＜tanx。

证明：构造函数

f(x)=x－sinx，

g(x)=tanx－x，x∈（0，），

则f'(x)=1－cosx＞0，

g'(x)=sec2x－1＞0。

所以f(x)，g(x)在（0，）内是单调递增函数，故f(x) ＞f(0)=0，g(x) ＞g(0)=0，

即x＞sinx，tanx＞x，

故sinx＜x＜tanx。

例2、已知m，n为正整数，且1＜m＜n。求证：（1+m）n＞(1+n)m。

分析：将待证不等式两边取对数，得nln(1+m) ＞mln(1+n)，即证明成立即可。

证明：构造函数

f(x)=，求导，得，所以f(x)在［2，+∞）上是减函数。由2≤m＜n知f(m) ＞f(n)，

即，

nln(1+m) ＞mln(1+n)，

所以ln(1+m)n＞ln(1+n)n，即（1+m）n＞(1+n)m。

例3、已知函数f(x)=x(x－a)(x－b)，其中0＜a＜b，设f(x)在x=s及x=t取到极值，其中s＜t，求证：0＜s＜a＜t＜b。

证明：易求得

f'(x)=3x2－2(a+b)x+ab。由f(x)在x=s及x=t取到极值，知s，t是二次方程f'(x)=0的两实根，

又f'(0)=ab＞0，

f'(a)=a2－ab=a(a－b) ＜0,

f'(b)=b2－ab=b(b－a) ＞0,即f'(x)=0在区间（0，a）与（a，b）内分别有一个实根。由s＜t及s，得二次方程f(x')=0的两实根，得0＜s＜a＜t＜b。

例4、设函数f(x)=ln(1+x)-x，

g(x)=xlnx，0＜a＜b，

证明：0＜g(a)+g(b)－2g()＜(b－a)ln2。

证明：由g(x)=xlnx，得g'(x)=lnx+1。构造函数F（x）=g(a)+ g(x)-2g()，则F'(x)=g'(x)-2[g()]'=lnx-ln。

当0＜x＜a时，F'(x) ＜0，所以F(x)在(0，a)内为减函数。当x＞a时，F'(x) ＞0，所以F（x）在(a，+∞)上为增函数。于是当x=a时，F（x）有极小值F（a）。因为F（a）=0，b＞a，所以F（b）＞0，

即0＜g(a)+g(b)-2g()。

设G（x）=F(x)-(x-a)ln2，则G'(x)=lnx-ln

=lnx-ln(a+x)。

当x＞0时，G'(x) ＜0，所以G（x）在(0，+∞)上为减函数。因为G（a）=0，所以G（b）＜0，即g(a)+g(b)-2g()＜(b-a)ln2。综上所述，0＜g(a)+g(b)-2g＜(b-a)ln2。