平面几何在培养学生逻辑能力上不是其他学科所能代替的，鲜明的直觉性和严谨的逻辑性使得几何成为数学竞赛选拔必不可少的内容。在这里笔者班门弄斧谈一下高中数学竞赛中平面几何的学习。

从应试的角度来说，首先是基础知识点和基本模型的认识，基础知识点包括联赛大纲中几个著名的定理（这几个定理都可以当成是面积法的结论），刚接触这几个定理的时候，最好了解多种证明方法，做下对比，思考每一种证法的关键，每一种方法给你带来的思维可能都不一样，平面几何的魅力也就是在于一个图形它可以从多种角度去理解它（或许就像薛定谔的猫？），对这些定理或者是基本模型的理解越深刻你的应用就会越熟练，要做到从“看山不见山”到“看山还是山”再到“看山不是山”的境界。

举个两个简单的例子：在下面的这个三角形中，点H为三角形ABC的垂心

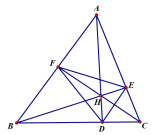
每个人可能得到的思维就不一样：

比如(1) 图里面有7个点（0.0废话吗？）

（2）有6组四点共圆

（3）H为三角形DEF的垂心

（4）H为三角形ABC的密克点，D为完全四边形AFHEBC的密克点

（5）三角形ABC以H为中心通过变换得到三角形DEF等等丰富的性质。

几何的学习过程我们也可以适当结合其他学科或者是日常生活的知识。

比如我们知道几何中有这样的一个定理：平面上有三个圆，每一对圆的外公切线交于一点，则这三个点共线。

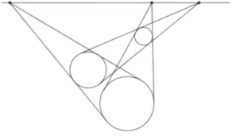
你可以这么理解：想象你站在一个无穷大的平面，有三个等大的球放在这个平面上，只不过由于有的球离你比较近，有的球离你比较远，这三个球看起来不一样大，每两个球确定了一个圆柱体，这三个横放在平面上的圆柱体无限延伸到无穷远，最后消失在地平线处。（现在这个定理好像是显然的）

可以先做一些各省预赛中的平面几何试题，一般用初中的平面几何知识点足以解决；接下来可以看《近代欧式几何学》或者《平面几何中的小花》这两本书，认识下一些新的概念和定理，看书的过程一定要有自己的思考，这才是数学竞赛的乐趣所在。

提高阶段推荐萧振纲老师的《几何变换与几何证题》，沈文选老师的《奥赛经典：几何分册》，如果时间充足的话可以再看市面上其他一些书，除了这些还需要掌握一些计算方法：三角法和复数。解析法不推荐。学习的过程一定要学会总结相关的题型，学会触类旁通，一道难的几何题往往是几个基本结论或者基本模型的综合。

可能很多同学会问是否可以通过当一只呆萌的“刷题狗”来提高自己的几何水平呢？我觉得答案是否定的。从数学教育的角度来看，解题既能给我们带来一定的乐趣，也具有相当的实用价值，解题的作用不能低估，但是这不意味着可以把学习数学与强化做题等同起来，这也是为什么我不推荐很多书的原因，因为题并非一律都有价值，一道好题是非常难得的，怎么样的题算一道好题呢？如果一道题目（甚至可以非常简单）可以让你启发出超越出题人本意的思想，那么我觉得这对你来说就是一道好题。总之，做几何题不应以数量为限，蜻蜓点水的做法绝不可取，而应秉着一种执着的态度，不倦的去探索。